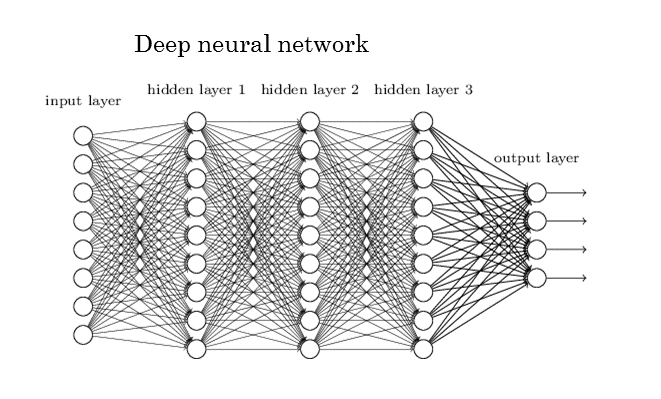
딥러닝하면 가장 먼저 접하는 저 신경망 그림은 뭔가 복잡해 보이지만 찬찬히 뜯어보면 비교적 단순하다.
위 그림을 직관적으로 받아들여보면 input layer는 우리가 예측 또는 분류할 때 쓸만할 것으로 예상되는 데이터에 해당한다. 즉 집값 예측이라고 한다면 평수, 방 개수 등등이 되겠다.
위 동그라미들을 이어주는 선들은 모두 가중치 $w$에 해당하며 1~8번 input 데이터에 각각 다른 가중치를 곱한 뒤 모두 더하는 내적을 수행한 결과가 hidden layer 1 이 된다.
식으로 표현하기 위해 input 데이터를 $x$라고 한다면 $w_1x_1 + w_2x_2....+b$ 로 표현이 된다.
이 식은 input이 8개 hidden layer 1이 9개 이므로 총 72개의 $w$가 필요할 것이지만 아무리 길어도 $w$가 최고차항이 1을 넘지 않는 1차 방정식에 머무르게 되므로 이 함수는 선형 모델에 머무르게 된다.
그렇게 되면 선형 모델이 가지고 있는 한계인 XOR 문제를 해결하지 못하게 되고, 이 세상에 선형함수로 해결할 수 없는 수많은 케이스에 대해 예측 또는 분류모델을 만들 수 없게 된다.
활성함수라고 불리는 Activation Function은 이러한 선형의 꼴을 꺾어주는 역할을 함으로써 더이상 선형함수가 아닌 함수가 되도록 한다.
그리고 각 layer층을 쌓을 때 마다 통상적으로 활성 함수를 적용하므로 그때마다 함수의 직선이 꺾인다고 생각하면 쉬울 것 같다.
활성 함수에 ReLU를 자주 쓰는 이유는?
활성함수는 Step function, Sigmoid, Tanh, ReLU...이렇게 줄줄이 발전해 오고 있지만 ReLU 함수 이후로 Gradient Vanishing 문제가 해결되었기 때문인지 아무생각없이 딥러닝 모델 구현 시 ReLU를 디폴트 값으로 쓰는 경우가 많을 것이다. 하지만 각 활성함수가 발전해온(?) 이유는 가중치 업데이트 이슈 때문이 가장 크다.
Back Propagation이라 부르는 역전파 알고리즘은 우리가 찾아야 할 $w$값을 찾아가는 여정이다.Back 이라는 단어가 쓰인 것처럼 가중치 업데이트는 DNN 연산 과정을 미분을 통해 거꾸로 밟아가게 된다.이 과정에서 활성 함수도 미분을 피할 수 없게 되는데 Step function, sigmoid, Tanh는 미분값이 매우 크거나 작을 경우 0에 근사하게 된다. 특히 sigmoid의 미분값으로 나올 수 있는 최대 값이 0.25에 해당하는데 가중치 업데이트 원리를 간단하게 말하자면 layer들의 가장 끝단에서 구한 실제값과 예측값의 오차값에다가 활성함수의 미분값을 곱하는 방식으로 바로 전단의 layer 오차값을 구하게 된다.
이 과정에서 집중해야할 부분은 활성함수의 미분값을 곱한다는 의미이다. 알다시피 소수 단위는 곱할수록 결과값이 점점 작아진다. 그렇기 때문에 sigmoid와 tanh와 같은 미분값은 많이 곱할 경우 0이라고 해도 좋을만큼 결과 값이 엄청 작아져 마치 사라진 것(Vanishing)과 다름이 없게 된다. 그렇게 되면 원래의 목적이었던 가중치 업데이트가 안되는 것이다.
ReLU Function의 경우 어떠한 값을 넣었을 때 양수라면 그 값을 그대로 뱉어내고 0 이하일 경우는 무조건 0이 으로 만드는 함수이다. 또한 미분값은 양수의 경우 무조건 1이 나오고 0 이하의 경우 무조건 0이 나온다.그렇기 때문에 가중치 업데이트 과정에서 오차값과 곱해지는 값이 0아니면 1이기 때문에 점점 사라지는 케이스는 없어지게 되고, 가장 첫 단의 가중치까지 잘 도달하게 된다.문제는 미분값이 0이 나오는 케이스다. 이 경우 가중치 업데이트가 아니라 그냥 단절이 된다. 0을 곱하면 그냥 0이 되기 때문이다. 해당 케이스가 발생하면 해당 뉴런 하나가 죽게 되고 만약 learning rate를 크게 설정하게 된다면 높은 비율의 뉴런이 죽어 학습 실패에 이르게 된다. 하지만 learning rate를 적절하게 설정한다면 소수의 뉴런이 죽게 되더라도 전체 학습에 큰 영향을 주지 않으므로 무시할만한 수준이 된다. 그리고 조금 다른 맥락이긴 하지만 오히려 일반화 성능을 높이기 위해 Drop out을 적용해 학습 시 의도적으로 뉴런 일부를 껐다가 켰다를 하기도 한다.그렇지만 멀쩡한 뉴런을 그냥 죽여버리는 것이 찝찝할 수 있기 때문에 나온 활성함수가 Leaky ReLU가 되고, 그 뒤로도 오만가지 활성함수가 존재하므로 DNN 모델 학습 시 발생하는 문제점이 어느 단에서 문제가 되는지 파악하고서 다른 함수를 적용하기 위해 각 함수들을 공부해 둘 필요가 있다.
'데이터사이언스 이론 공부' 카테고리의 다른 글
| 엔트로피(Entropy)와 크로스 엔트로피(Cross Entropy) (0) | 2022.10.07 |
|---|---|
| NDCG로 랭킹 추천모델 평가하기 (0) | 2022.09.15 |
| 하이퍼 파라미터 튜닝에 관하여 (0) | 2022.09.13 |
| MAP(Maximum A Posterior) 에 대한 이해 (0) | 2022.09.08 |
| GitHub 실전 예시를 통해 실무 활용법을 파악해두자 (0) | 2022.09.06 |