Attention Mechanism

📌 번역 대상에 대한 정보를 다 담은 최종 $h$를 가지고 디코딩 과정에 들어갈 때 $h_0$ 에서 $h_t$까지 각각의 단계에서 획득한 정보를 들고 와서 참고하자는 아이디어에서 시작되었다.(장기의존성 문제 해결을 위한 방안) 이때 각 단어의 번역 과정($s$)에서 연관성이 가장 높은 $h_t$를 파악해서 $s$가 추가로 참고한다는 점이 핵심이다.
Dot-Product Attention
📌 가중합/가중평균
디코딩 과정에서 각 단어의 예측 시 어떤 h를 참조하는게 좋을지 구분할 수 있어야 한다. 이를 위해서 가중합/가중평균 계산이 적용된다.
→ 예를 들어 학창 시절 중간고사 반영비율 25% 기말고사 35%, 실기 40%처럼 특정 분야에 대한 반영 비율이 $w$에 담겨 각 $h$에 적용된다면 어떨까? 그래서 각각의 $h$에 곱할 $w$들의 총합이 1이 된다면, 그 $w$는 각$h$별 중요도를 대변하는 역할을 하게 된다. 그래서 $w$가 어떤 비율로 구성이 되느냐에 따라 $h$의 중요도가 정해진다고 볼 수 있다. 그렇게 반영비율이 적용된 최종 점수를 계산하는 행위를 우리는 가중평균을 구한다고 말한다.
→ 그러면 우리가 보통 시행하던 가중합(w에 벡터를 곱해서 더하는 내적)이 곧 가중평균을 구하는 것과 동일해 진다.
📌 Dot-Product
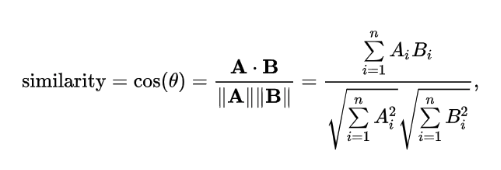
두 벡터를 내적하는 것을 의미한다. 이 과정은 코사인 유사도 연산의 분자에 해당한다.
그래서인지는 몰라도 Dot-Product를 수행하면 A, B 벡터가 얼마나 유사한가를 볼 수 있다고 한다.
코사인 유사도 공식을 보면 두 벡터의 dot product를 각 벡터의 크기의 곱으로 나누는 것을 확인할 수 있는데... 벡터에 대한 지식이 부족한 나로서는 우선 dot product가 유사도 의미를 담는다 정도로 이해하고 넘어갔다.
📌 softmax

$e_i$는 디코딩 과정에서의 첫번째 단어($q$)와 인코딩 과정에서 각 단어 학습 시 얻은 $h_1$ ~ $h_k$ 간 유사도를 구한 값들이 된다.
$w_i$는 $e_i$들을 softmax에 적용함으로써 모든 $e$의 합이 1이 되게 하여 위에서 말한 바와 같이 유사도가 높은 정도를 비율로서 표현할 수 있게 된다. 이를 가중치($w$)로서 사용하고자 하는 의도이다.
$a$는 디코딩 과정에서의 각 단어($v_i$)가 $h_1$ ~ $h_k$ 중 어떤 $h$를 높은 비중으로 참조하는 것이 좋을지 판단해주는 $w_i$를 가중합하여 유사한 정도가 반영된 가중평균값을 구하게 되고 그 값이 Attention Value가 된다.
Seq2seq with Attention

→ 위에서 구한 Attention Value는 결국 디코딩 과정에서 각 단어(s) 하나와 h들 간 유사도에 따른 가중치가 반영된 가중평균에 해당하며 이 결과는 s에 concat한다.
→ concat의 결과를 토대로 예측을 위한 최종 fc에 넣어 예측값 $\hat{y}$을 얻도록 하고, 그 결과는 다음 s의 인풋으로 사용된다.
📌 Attention Map

위와 같이 Attention Value를 얻은 연산을 통해 번역 전후 state간 유사도 측정을 하므로 “어떤 단어를 해석하는데 있어 어떤 단어를 많이 참고했는지”에 대한 사후 해석이 가능해 진다는 장점이 있다.
📌 정리
위에서는 디코딩 과정에서 첫번째 단어($s_1$)에 대한 Attention Value 도출에 대해 설명했지만 실제로는 모든 단어($s_1$ ~ $s_T$)에 대해서 적용한다는 점을 기억하자
'데이터사이언스 이론 공부' 카테고리의 다른 글
| BERT 모델에 대한 기본이해 (0) | 2022.12.12 |
|---|---|
| Transformer(트랜스포머)에 대한 간략 정리 (0) | 2022.12.05 |
| RNN과 Encoder-Decoder Structure (0) | 2022.12.05 |
| RNN과 LSTM 원리에 대한 간략 정리 (0) | 2022.12.05 |
| 딥러닝 기초 용어에 대한 간단 정리 (0) | 2022.11.02 |